PICでFFT (XC16でFFTにトライ)
<バンドスコープ、自作,PIC>
デジタルオシロスコープが基本動作としては、可能になり、ADCでデータを取り込む方法、そのデータをTFT LCD上に表示する方法が可能になりましたので、次はいよいよFFTにトライします。 WEB上で色々検索した結果、FFTのいろはも良く判っていない輩にとっては、どれも思考がついていかない為、PICで実行が可能かも知れない大浦先生のC言語によるパッケージを検討する事にしました。 このパッケージは、標準的なC言語で作成されており、該当する変換関数を1回実行すれば、回転因子の作成や、ビットリバースなど全部関数の内部でやってしまい、処理完了したら、入力した同名の配列にFFT結果を返すというもので、中身をよく知らない私には打ってつけのソースです。
さっそく、先生のホームページから、zipファイルをダウンロードし、解凍すると、沢山のファイルとテスト用のサンプルまで同梱されていました。
fftsgと言われる、大浦先生のソースは、XC16でも問題なくコンパイルできます。 動作テスト以前の問題として、全ソースがXC16でコンパイルできるか試したところ、すべてOKでした。
今回、これらのソースをインストールするのは、PIC24FJ64GA002です。 プログラムメモリーは64Kありますが、RAMが8Kしかなく、PICKit3経由でターゲットPICを決め、いざ、コンパイルすると、データメモリー不足で即エラーになります。 トライしたのは、沢山のプログラムの中で、一番高速だと言われるfftsg.cでした。 浮動小数点がdoubleで表現されているので、これをすべてfloatに置換してトライしましたが、やはりダメでした。 そこで、プログラムをfft4g.cに代えてトライすると、メモリー使用量88%でやっとコンパイル成功しました。 大浦先生の解説では、このプログラムが有名なCooley-Tukey 型 FFTで基数型とも言われるものらしく、コンパイルに失敗したソフトはこれより高速なSplit-Radix型と言うものらしい。
高速に越した事はありませんが、コンパイル出来なければ話になりませんので、今回はfft4g.cで進める事にします。
先に、FFTが成功し、例の320x240TFT LCDに表示できたところを紹介し、そこまでの工程を以下説明します。
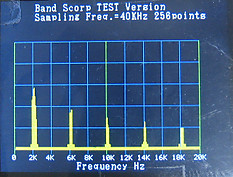
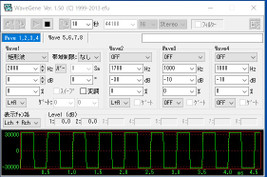
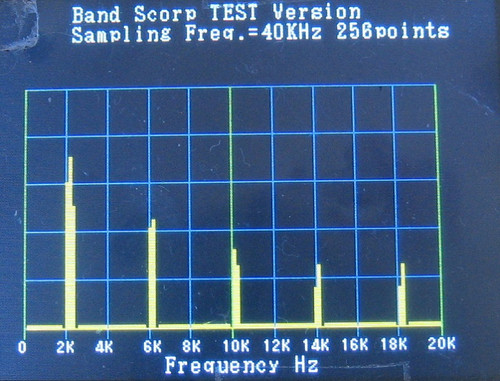
左上が、2KHzの矩形波をFFTして、そのスペクトルを表示したものです。 源信号は矩形波ですので、奇数次の高調波がきれいに並んでいます。 右上が、ウェブジェネレーター(WG)で発生させた2KHzの源信号です。 左上の画像で、水平方向は、2KHzスパンでメモリを合わせましたが、垂直方向は校正されていません。単位はdBです。
このc言語のパッケージは、オリジナルがdoubleの浮動小数点形式で作成されており、小規模なマイコン用ではなく、windows95が出たころのPC用に作られていると思われ、メモリーはかなりセーブしているように見えますが、16bitのPICには、まだ無理があります。 そこで、浮動小数点をfloatに代えて、メモリーの量とスピードをなんとかカバーしなければなりません。
FFTを実行する場合、サンプリング数が最小分解能を決めますが、この数は2のn乗でなければなりません。 今回は、LCDの横のピクセルサイズが320しかありませんので、これ以上多くしても表示は同じになります。 そして、320以内に収まる2のn乗の最大値は256ですので、FFTも256個のサンプル数で進めます。 また、サンプリング周波数ですが、バンドスコープで表示しようとしているIF帯域のキャリア周波数が約9.8KHzですから、最高で20KHzまで表示出来たらよいので、サンプリング周波数はその2倍の40KHzくらいで良い事になります。
従い、PICのADCはタイマー3から40KHzの周期で割り込みをかけ、そのたびにADCから10bitのデータを取り出し、これを256個だけメモリーに格納し、割り込みを中止した後、このデータをFFT関数に渡してFFT処理してもらいます。
FFT関数はa[]という配列変数に、「実数」「虚数」「実数」「虚数」・・・の順にサンプル数の2倍の配列数となっており、今回はa[512]の配列となります。 今回のFFTでは、虚数は使いませんので、ADCで得られたfloatのデータを実数部分に、0.0のデータを虚数部分に代入したあと、FFT関数に渡してやれば良いわけです。 下のfor文がそれを実行しているところです。 ADCの出力は符号付きintで取得し、これを512で割って、floatに変換し、a[]に代入しています。 途中のadfloatの変数は、CASTの不安定さを取り除くために、挿入したダミー変数です。これを中継して行わないと、時々プログラムがおかしくなります。
for (k=0;k <256;k++) {
adfloat=(float)ADdata[k]/512;
adfloat = adfloat * hanning256[k];
a[k*2]=adfloat;
a[k*2+1]=0.0;
}
hanning256[k]はハニング窓関数で、この処理をしていないと、左の画像のごとく、低い周波数のすそ野が広がってしまいますので、必ず実行します。
このハニング関数は、エクセルで計算し、それをhanning256.hというファイルに編集してあります。
エクセルファイルの実物は、後で、ダウンロードできるようにしておきます。
このパッケージの中には、FFTの関数として、以下の2つの関数が紹介されています。
cdft: 複素離散フーリエ変換
rdft: 実離散フーリエ変換
両方とも実験したところ、スペクトルが細くなるのがcdftの方で、rdftの場合、窓関数を掛けても左上の窓関数なしのcdftくらいにしかなりませんでした。 また、両方ともメモリーの使用量は同じくらいでしたが、rdftの方が、処理速度が速いようです。 しかし、この実験ではcdftで進行します。
FFTを実行すると、a[]の中に結果が格納されて終了しますが、このデータの中で周波数スペクトルを表す実数はプラスとマイナスが有り、256ポイントの0から127ポイントまでが正の周波数を表し、128から255ポイントまでが負の周波数を表します。 今回の目的は0から20KHzまでの周波数スペクトルを256ピクセルのグラフで表す事ですので、負の周波数のデータが必要ありません。 従いa[]の0番目から127番目までの実数データだけを二乗平方根して、これを256ピクセルに棒グラフで表せれば良いのですが、グラフ画面のチラツキが激しく、安定したスペクトルを見る事が出来ません。 ちなにみ、実数の隣にある虚数を含めて二乗和の平方根とすると、かなり安定した、グラフが得られます。 バンドスコープとしては、この安定した状態のほうが見やすいので、この方法でグラフ表示する事にします。
用意したLCDの表示ピクセルは256ですから、結果的にふたつのピクセル列に同じデータを書き込む事になります。256のピクセルを有効活用しようとすれば、ADCのサンプリング数を512にすれば良いのですが、それを実行すると、即メモリー不足でエラーになりますので、このPICでは出来ません。
この、グラフの縦の目盛は対数としますので、二乗和は行いますが、平方根は実行しません。 この結果対数計算値は平方根を実行した場合の2倍になりますので、この結果に10を掛け算すると電圧レベルのdB値になります。
for (k = 0;k <= 127;k++) {//FFT結果の負の周波数は無視する。
j0=a[k*2];j1=a[k*2+1];
lvl=(int)4*(10*log10f(j0*j0+j1*j1));
lvl = Goffset - lvl;
if (lvl > DSdata[k]) {
write_HVline(m,DSdata[k],m+1,lvl,backcolor);//xs<=xe ys<=yeの事
}
write_HVline(m,lvl,m+1,208,linecolor2);//xs<=xe ys<=yeの事
DSdata[k] = lvl;
m=m+2;
}
この辺の計算式は1行で済ませるより、一度変数に格納してから、処理させると、実行時間が早くなるようです。
また、X方向に2ピクセルだけグラフデータを棒グラフで書き込む前に、前回書き込んだデータを消しますが、消す範囲は、今回のレベルより前回のレベルが高い場合のみで、かつ今回分から高かった表示のみ消していますので、グラフ画面全体のチラツキも最小限になっています。
ここまでやって先に紹介したようなスペクトルグラフが得られるわけですが、その処理時間は、実用レベルとはかけ離れていました。
FFTの計算時間は約78msecかかりました。
FFTの計算を含んだLCD描画時間は約120mescでした。
この時間では、実用は無理です。少なくと、現在の120msecを30msec以下にしないとダメでしょう。
結局、Tcyが16MHzの16bitマイコンでは、無理と判りましたので、もっと早く実行できるPIC用のソフトをさがすか、32bitマイコンに乗せ換えるか考えねばなりません。
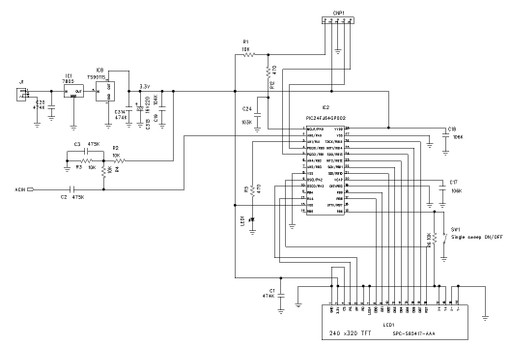
今回の配線図です。
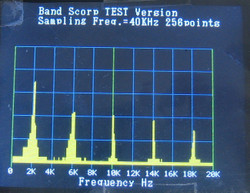
上は、表示レベルを拡大したもので、縦方向のメモリが10dB/divくらいになっています。
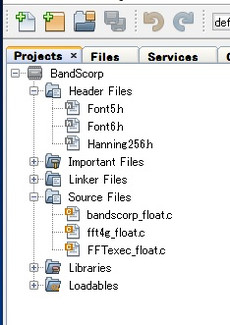
この実験に使ったすべてのソースファイルです。 MPLAB Xのプロジェクトは左のようなファイル構成になっています。
ハニング窓関数を作成するエクセル Hanning_coef.xlsxをダウンロード
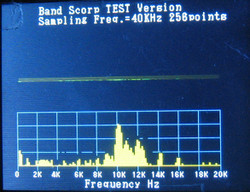
完成ではありませんが、20KHzまでのスペアナができましたので、自作のSSBトランシーバーの2nd IFの出力につないでみたのが左の画像です。 使ったプログラムは上のソースファイルとは異なる実験用なので、上のソースファイルで左の画像が得られるわけでは有りません。
キャリア周波数が9.766KHzですから、その周波数を中心に+/-4KHzくらいは、反応があるはずと見てみると、LSBとUSBが反転しています。 これは、その通りで7MHzのLSB信号は、2nd IFでは反転し、USBになっていますので、この場合、負の周波数を表示しないと、グラフの周波数が逆になってしまう事を納得。
また、真ん中より少し上に淡い水平一直線のオビが見えますが、これは、ウォーターフォールのディスプレイを実験的に行ったものです。 たった5行のウォーターフォールですので、何がなんだかわかりませんが、このPICの残り少ないRAMを使って作りましたので、これが限界です。 それと、ウォーターホールを含めた、MAINルーチンの1周時間は140msecくらいになってしまい、スペクトルが見慣れたPCのバンドスコープのようには見えません。 この第2IF信号を使ったバンドスコープをしばらく見ていましたが、表示される範囲は、ルーフィングフィルターとなる24MHzのクリスタルフィルターの帯域内のみで、+/-3KHzが表示されるだけです。 HDSDRを経験した身としては、面白くありません。 せっかく作るなら、せめて+/-50KHzくらいはカバーしたい。
これらの課題を抱えて、実用的なバンドスコープをどうやって作るか再検討する事にします。